Solution Given f 2, ∞) → B defined as f (x) = x 2 − 4 x 5 for all x = 2, 3, where f (x) is bijection Since, f (x) is bijection (ie 1 1 and onto) ∴ Codomain of f (x) = Range of f (x) ⇒ Range of f (x) = B Now, Let y = x 2 − 4 x 5 ⇒ x 2 = y 4 x − 5 ⇒ x 2 − 4 x 5 − yLet A and B be two sets show that f A × B → B × A s u c h t h a t f (a, b) = f (b, a) is a bijective function View solution Let a function f defined from R R as f(x)= x p 2 , p x 5 , for x ≤ 2, for xSee the answer Determine whether each of these functions from R to R is a bijection Find its inverse function if it is a bijection 1 f (x) = 2x 4 2 f (x) = −x 2 − 2 3 f (x) = x 2 2/x 2 1

State Which Of The Following Are One One And Onto Function F R Gtr Defined By F X 2x 1 Youtube
F(x)=x/x^2+1 is bijective
F(x)=x/x^2+1 is bijective-Minimum f = 463, nearly This is improved to 8sd, \displaystyle {} , using an iterative numerical methodGiven that f(x) = x/(1 x^{2}) Taking the derivative of f(x) we get f'(x) = (1 x^{2} 2x^{2})/ (1x^{2})^{2}= (1x^{2})/(1x^{2})^{2} = since for all real x, 1 x^{2} is positive and also the denominator is also positive this implies derivative




Ex 1 2 7 State Whether One One Onto Or Bijective Class 12
/09/17 · For a given x ∈ A, there is exactly one y ∈ B such that y = f(x) The definition of a function does not require that different inputs produce different outputs That is, it is possible to have x1, x2 ∈ A with x1 ≠ x2 and f(x1) = f(x2) The arrow diagram for the function f in Figure 65 illustrates such a function · 4 I have to show that the function f ( − 1, 1) → R f ( x) = x x 2 − 1 is bijective I have shown that it is injective which is pretty simple I'll write it out here for future reference To show that f is injective, let x 1, x 2 ∈ ( − 1, 1) Assume that f ( x 1) = f ( x 2) ThenAnswered 2 years ago · Author has 259 answers and 1657K answer views f (x) = 1/x is both injective (onetoone) as well as surjective (onto) f R to R f (x)=1/x , f (y)=1/y f (x) = f (y) 1/x = 1/y x=y Therefore 1/x is one to one function that is injective Let f (x)=y 1/x = y
Equivalence Relations and Functions October 15, 13 Week 1314 1 Equivalence Relation A relation on a set X is a subset of the Cartesian product X£XWhenever (x;y) 2 R we write xRy, and say that x is related to y by RFor (x;y) 62R,we write x6Ry Deflnition 1 A relation R on a set X is said to be an equivalence relation if · Putting f(x1) = f(x2) we have to prove x1 = x2 Since if f (x1) = f (x2) , then x1 = x2 ∴ It is oneone (injective) Check onto (surjective) f(x) = x3 Let f(x) = y , such that y ∈ N x3 = y x = 𝑦^(1/3) Here y is a natural number ie y ∈ N Let y = 2 x = 𝑦^(1/3) = 2^(1/3) So, x is not a natural number ∴ f is not onto (not surjective) Hence, function f is injective but not surjectiveAnswer ∴ f is an oneone function Then, y =1 The function f is onto if there x ∈ A such that f (x) = y ∴ f is onto Since f is one=one and onto then, the given function is bijective
We take the old exponents and subtract one, so it's gonna give us a negative three, which means that we end up getting negative two x to the negative three Now, another thing is we want to evaluate it at a so f prime of a is just going to be a negative to a to the negative three And this will be our final answer for this problem Add To PlaylistAlternatively, f is bijective if it is a onetoone correspondence between those sets, in other words both injective and surjective Example The function f(x) = x2 from the set of positive real numbers to positive real numbers is both injective and surjective Thus it is also bijectiveThe Function F a → B Defined by F (X) = X2 6x 8 is a Bijection If (A) a = ( ∞ , 3 and B = ( ∞, 1 (B) a = 3 , ∞) and B = ( ∞, 1 a = ( ∞ , 3 0 Department of PreUniversity Education, Karnataka PUC Karnataka Science Class 12




Prove That The Function F N N Defined By F X X 2 X 1 I




Let F C Rightarrow D F X X 2 X 9 F Is Chegg Com
1) = f 1(f(x 1)) = x 1 et f 1(u 2) = f 1(f(x 2)) = x 2 L'implication à montrer s'écrit donc f(x 1) f(x 2) carfestcroissanteLecaractèrecontinudef 1,plustechnique,n'estpasdémontréici Remarque Le point a) est une conséquence du TVI et est essentiel pourThe function f R → R defined by f(x) = 2x 1 is surjective (and even bijective), because for every real number y, we have an x such that f(x) = y such an appropriate x is (y − 1)/2 · Prove that a function f R → R defined by f ( x) = 2 x – 3 is a bijective function Explanation − We have to prove this function is both injective and surjective If f ( x 1) = f ( x 2), then 2 x 1 – 3 = 2 x 2 – 3 and it implies that x 1 = x 2 Hence, f is injective So, x = ( y 5) / 3 which belongs to R and f ( x) = y Hence, f is




F Pi2 Pi2 1 1 F X Sin X Is
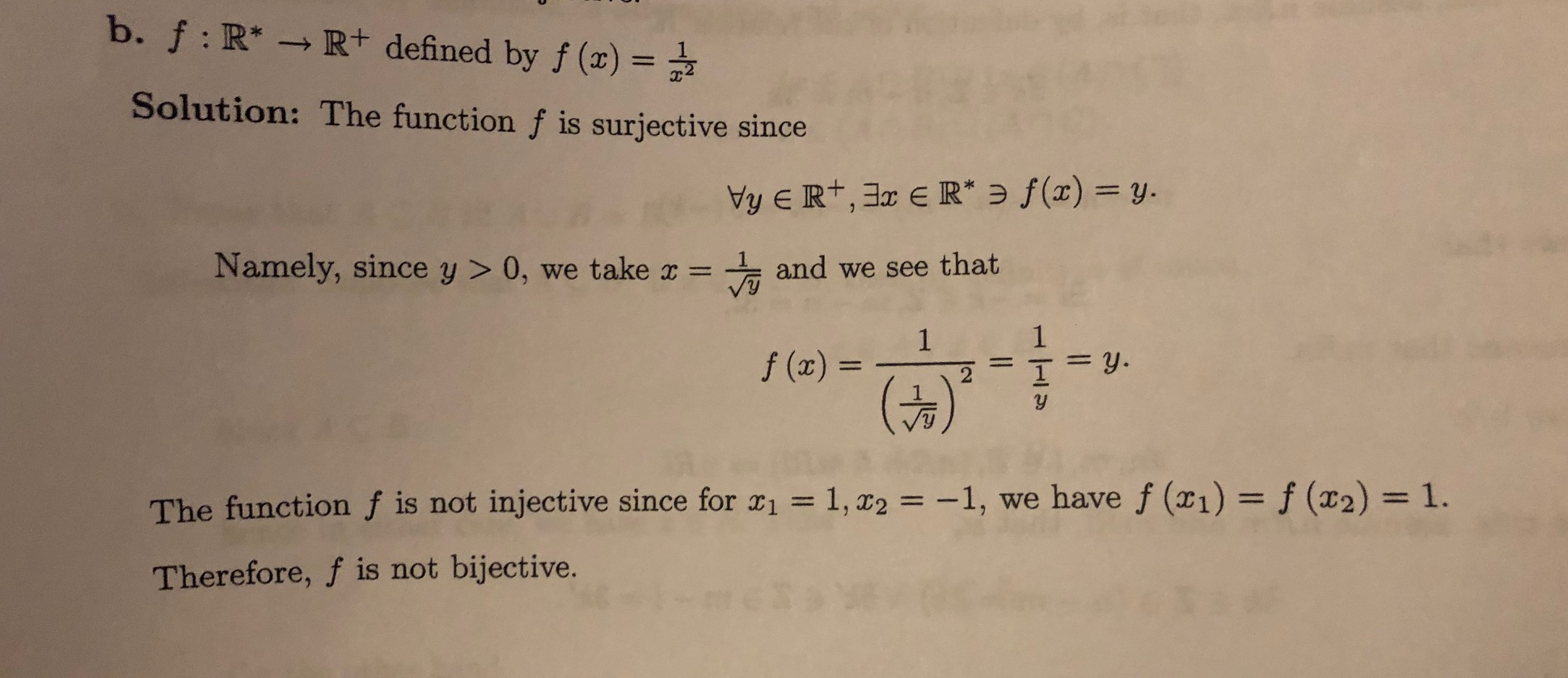



B F R R Defined By F X Solution The Function F Chegg Com
The Function F X X 1 X Has The Function F X X 2 E X Increases In The Interval The Function F X Y Defined By F X Sinx Is One One But Not Onto If X And Y Are Respectively Equal To Leave a Comment Cancel reply Your Mobile number and Email id will not be published Required fields are marked * * Send OTP · asked May 19, 19 in Mathematics by Jagan (211k points) If the function f R – {1, – 1} → A defined by f (x) = x2/1 x2, is surjective, then A is equal to (1) R – {– 1} (2) R – – 1, 0) (3) R – (– 1, 0) (4) 0, ∞) jee mains 19 Please log in or register to add a commentExample 462 The functions f R → R and g R → R (where R denotes the positive real numbers) given by f ( x) = x 5 and g ( x) = 5 x are bijections Example 463 For any set A, the identity function i A is a bijection Definition 464 If f A → B and g B → A are functions, we say g is an inverse to f (and f is an inverse to g




Ex 1 2 7 State Whether One One Onto Or Bijective Class 12




Let F Be A Function Defined By F X X 1 2 1 Xge1 S
· #f(x)=x^24# In order for #f# to have an inverse, it must be a bijection That is, it must be an injection and a surjection So we must restrict the domain and codomain appropriately It is standard that the square root operation returns positive values, soBut let's use "f" We say "f of x equals x squared" what goes into the function is put inside parentheses after the name of the function So f(x) shows us the function is called "f", and "x" goes in And we usually see what a function does with the input f(x) = x 2 shows us that function "f" takes "x" and squares itRD Sharma Solutions, Maths Chapter 2, for Class 12, help students who aspire to obtain a good academic score in the exam The solutions are designed by experts to boost confidence among students in understanding the concepts covered in this




Ex 1 2 10 F X X 2 X 3 Is F One One Onto Class 12




Show That The Function F R R Defined By F X 3x 3 5 For All X In R Is A Bijection Youtube
BIJECTION Function It states that when the function is one to one and onto then the function bijection function So, first, we need to show function is one to one To show that the function is o view the full answerDetermine whether f(x) = (x1)/(x2) is a bijection from R to R R denoted the set of all real numbers Explain your answer 848 PM Determine whether f(x) = −3x^2 7 is a bijection from R to R R denoted the set of all real numbers · Ex 12 , 7 In each of the following cases, state whether the function is oneone, onto or bijective Justify your answer f R → R defined by f(x) = 3 − 4x f(x) = 3 – 4x Checking oneone f (x1) = 3 – 4x1 f (x2) = 3 – 4x2 Putting f(x1) = f(x2) 3 – 4x1 = 3 – 4x2 Rough Oneone




Discrete Mathematics Solutions To Homework 12 For Each Of The Following Sets Determine Whether 2 Is An Element Of That Set Pdf Free Download




Notes On Topics Of Algebra Notes
Example 1 The function f (x) = x 2 from the set of positive real numbers to positive real numbers is injective as well as surjective Thus, it is also bijective Thus, it is also bijective However, the same function from the set of all real numbers R is not bijective since we also have the possibilities f (2)=4 and f (2)=4Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history




Bijective Function Simple English Wikipedia The Free Encyclopedia




Solved Let X Be The Set Of Odd Integers Let F X Z Be T Chegg Com
F(x) = 1/x, g(x) = 1/xThe rule f(x) = x 2 is a bijection if the domain and the codomain are given by (a) R,R (b) R, (0, ∞) (c) (0, ∞), R (d) 0, ∞), 0, ∞)For any set X, the identity function id X on X is surjective;




Notes On Topics Of Algebra Notes




Prove That The Function F Nvecn Defined By F X X 2 X 1
So, f(x) is not onto Therefore, f (x) is not bijective (ii) So, g(x) is not oneone Also, Hence, the range is 0, 1, which is subset of codomain 'A' So, f(x) is not onto Therefore, f(x) is not bijective (iii) Hence, f(x) is oneone Hence, the range is 1, 1 So, h(x) is onto Therefore, h(x) is bijective (iv) Therefore, k(x) isIn mathematics, a bijection, bijective function, onetoone correspondence, or invertible function, is a function between the elements of two sets, where each element of one set is paired with exactly one element of the other set, and each element of the other set is paired with exactly one element of the first set There are no unpaired elements In mathematical terms, a bijective function f X → Y is a onetoone (injective) and onto (surjective) mapping of a set XThe function f is defined by f (x) = x4 −4x2 x 1 for −5 ≤ x ≤ 5 What is the interval in which the minimum of value of f Purely a graphical approximation;




Today S Topics Proof That A Given Function Is Injective Or Surjective Composite Functions Properties Of The Composite Functions Inverse Functions Proofs Ppt Download




Show That The Function F R R Defined As F X X 2 Is Neit
The function f Z → {0, 1} defined by f(n) = n mod 2 (that is, even integers are mapped to 0 and odd integers to 1) is surjective;Classify the Following Functions as Injection, Surjection Or Bijection F R → R, Defined By F(X) = `X/(X^2 1)` 0 Department of PreUniversity Education, Karnataka PUC Karnataka Science Class 12 · Let \(f 0, α) → 0, α) \) be defined as \(y = f(x) = x^2\) Is it an invertible function?




Cs100 Discrete Structures Ppt Download




Determine The Function F R R Define By F X X If X Gt 2 5x 2 If X 2 Is A Injection Or Surjection Brainly In
Solve for x x = (y 1) /2 Here, y is a real number When we subtract 1 from a real number and the result is divided by 2, again it is a real number For every real number of y, there is a real number x So, range of f(x) is equal to codomain It is onto function Hence it is bijective function (ii) f R > R defined by f (x) = 3 – 4x 2 SolutionHence, the function f(x) is surjective Hence, since the function is both injective and surjective over the given domain and range, then the function is a bijection Approved by eNotes Editorial Team · if a function f 2 infinity b defined by f x x 2 4x 5 is a bijection then b 0bq55buu Mathematics TopperLearningcom




Ex 1 2 2 Check Injectivity And Surjectivity Of I F X X 2




Prove The Function F Z X Z Z Given By F M N 2m N Is Onto Surjective Youtube
If so find its inverse Solution Yes, it is an invertible function because this is a bijection function Its graph is shown in the figure given below Let y = x 2 (say f(x)) \(\Rightarrow x = \sqrt{y}\) But x can be positive, as domain of f is 0, α)This problem has been solved!Dann ist f nicht injektiv, nicht surjektiv und auch nicht bijektiv Da fehlt immernoch N, aber das soll dann wahrscheinlich einfach das Bild von f sein Dann ist f injektiv, surjektiv und bijektiv Für die Umkehrabbildung müsstest du f (x)=x 2 1=y nach y umstellen



How To Prove The Rational Function F X 1 X 2 Is Surjective Onto Using The Definition Youtube




Rd Sharma Solutions For Class 12 Maths Chapter 2 Function Download Free Pdf
A function f1 B → A is called the inverse of f if the following is true ∀a ∈ A ∀b ∈ B (f(a) = b ↔ f1(b) = a) In other words, if f maps a to b, then f1 maps b back to a and viceversa Not all functions have inverses (we just saw a few examples of functions with no inverse) If f is a function that has an inverse, then we say thatTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW If `2f (x1)f((1x)/x)=x , then f(x)` isQuestion # 1 Determine whether each of these functions is a bijection from R to R a) f (x) = 2 x 1 b) f (x) = x2 1 c) f (x) = x3 d) f (x) = (x2 1 )/ (x2 2) check_circle




Discrete Mathematics Solutions To Homework 12 For Each Of The Following Sets Determine Whether 2 Is An Element Of That Set Pdf Free Download




Show That F R R Defined As F X X 3 Is Bijection Maths Relations And Functions Meritnation Com
F(x) = 1 e x Theorem 271 If a function is a bijection, then its inverse is also a bijection Proof Let f A!e a bijection and let f 1 B!Abe its inverse To show f 1 is a bijection we must show it is an injection and a surjection Let x 1;x 2 2e such that f 1(x 1) = f 1(x 2) Then by the de nition of the inverse we have x 1 = f(f 1(xThis is equivalent to saying if f (x 1) = f (x 2) f(x_1) = f(x_2) f (x 1 ) = f (x 2 ), then x 1 = x 2 x_1 = x_2 x 1 = x 2 A synonym for "injective" is "onetoone" The function f Z → Z f\colon {\mathbb Z} \to {\mathbb Z} f Z → Z defined by f ( n ) = 2 n f(n) = 2n f ( n ) = 2 n is injective if 2 x 1 = 2 x 2 , 2x_1=2x_2, 2 x 1 = 2 x 2 , dividing both sides by 2 2 2 yields x 1 = x 2 x_1=x_2 x 1 = x 2



How To Determine If A Function Is One To One Mathematics Stack Exchange




Ex 1 2 7 State Whether One One Onto Or Bijective Class 12




Surjective Onto And Injective One To One Functions Video Khan Academy




F R R Given By F X X Sqrt X 2 Is A Injective B Surj



The Function F R Gt 1 2 1 2 Defined As F X X 1 X 2 Is Youtube




State Which Of The Following Are One One And Onto Function F R Gtr Defined By F X 2x 1 Youtube




Q 16 Classify The Following Functions F X Defined In Rrarrr As Injective Surjective Both O Youtube




If The Function F R 1 1 To A Definded By F X X 2 1 X 2 Is Surjective Youtube




Example 11 Show F X X2 Is Neither One One Nor Onto Examples




The Function F Rvec 1 2 1 2 Defined As F X X 1 X 2 Is




Relation And Function Ppt Download




Solved Prove That The Function F R Rightarrow R Given B Chegg Com




Which Of The Following Are Injections Or Surjections Or Bijections Justify Your Answers F R R Defined By F X 2x Lar I F R 0 00 Defined By F X 2




Let F X X Root 1 X2 Show That Fofof X X Root 1 3x2 Brainly In




Let F R Rightarrow R Be A Function Defined By F X X X N Where Represents Fractional Part Function N 1 Injective N 2 Surjective N 3 Bijective N 4 Not Bijective




Notes On Topics Of Algebra Notes




Tutorial 4 Questions Wix 1001 Mathematics For Computing Semester 15 16 Tutorial Functions Consider Function With Domain Codomain And The Rule X2 Draw Studocu




Let A X Xepsilonr F Is Defined From Ararrr As F X 2x X




Ex 1 2 2 Check Injectivity And Surjectivity Of I F X X 2




Misc 4 Show F X X 1 X Is One One Onto Miscellaneous




Functions Lecture Notes 6 Studocu




Help Maths




Domain Of F X Log 1 X Sqrt X 2 1 Youtube




State Whether The Function Is One One Onto Or Bijective F R R Defined By F X 1 X2 Brainly In




Which Of The Following Functions From Z To Itself Are Bijections




If The Function F X X 2 Bx 3 Is Not Injective For Values Of




Prove That The Function F X 3x 2 Is A Bijective Mapping Brainly In




Example 12 Show That F X X 1 If X Is Odd X 1 If X Is Even




Problem 1 Determine Whether Each Of These Functions Chegg Com




If A 2 1 0 1 2 And F A B Is A Surjection Defined By F X X X 1 Then Find B Brainly In




Solved 3 Let F R R F X X2 X 1 And Show That F Is No Chegg Com




Bijection Function F X Y X Y 1 2x 2y 2 Mathematics Stack Exchange
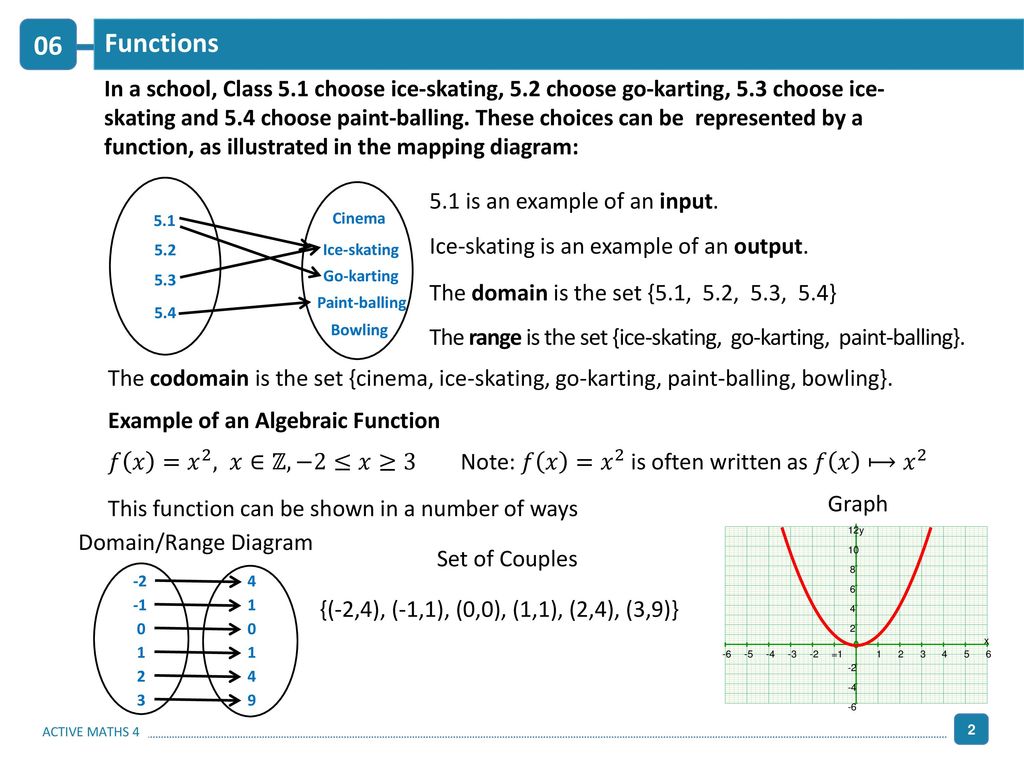



Chapter 6 Functions 06 Learning Outcomes Ppt Download




Classify Each Function As Injective Surjective Chegg Com




Rd Sharma Solutions For Class 12 Maths Chapter 2 Function Download Free Pdf
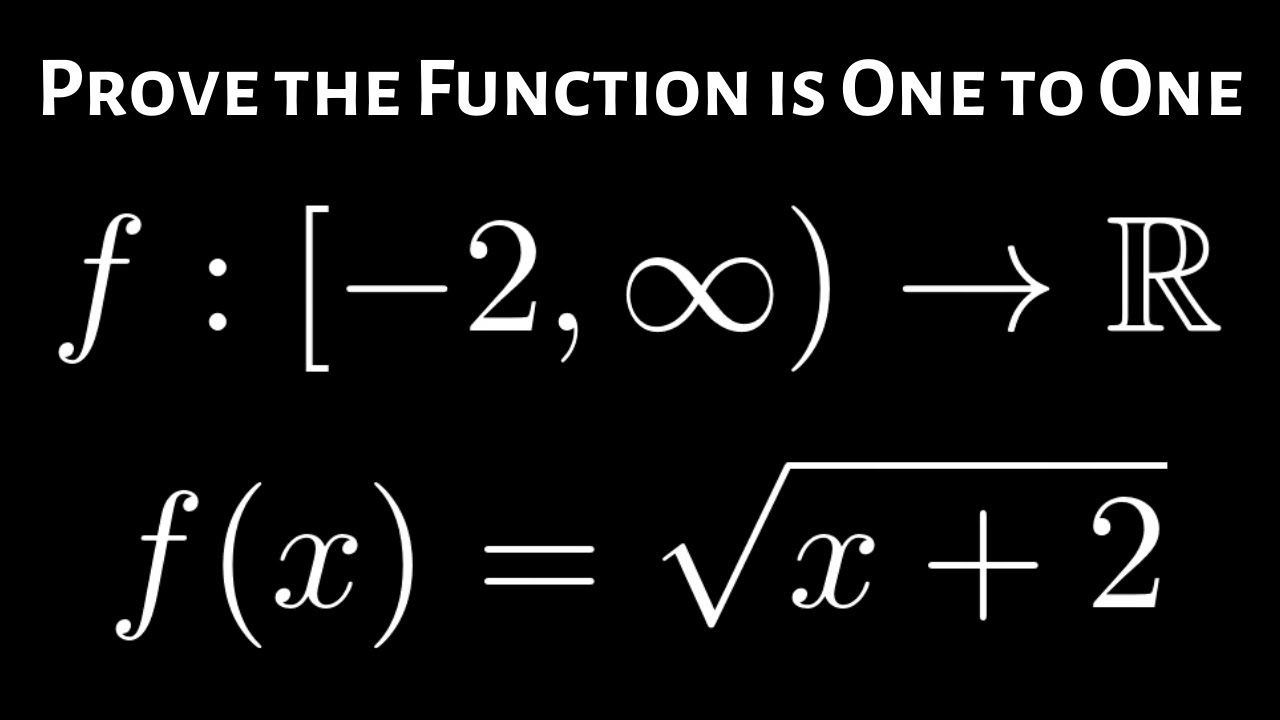



Proving The Function F X Sqrt X 2 Is One To One Injective Using The Definition Youtube




Solved Problem 1 Points Consider The Following Set Chegg Com
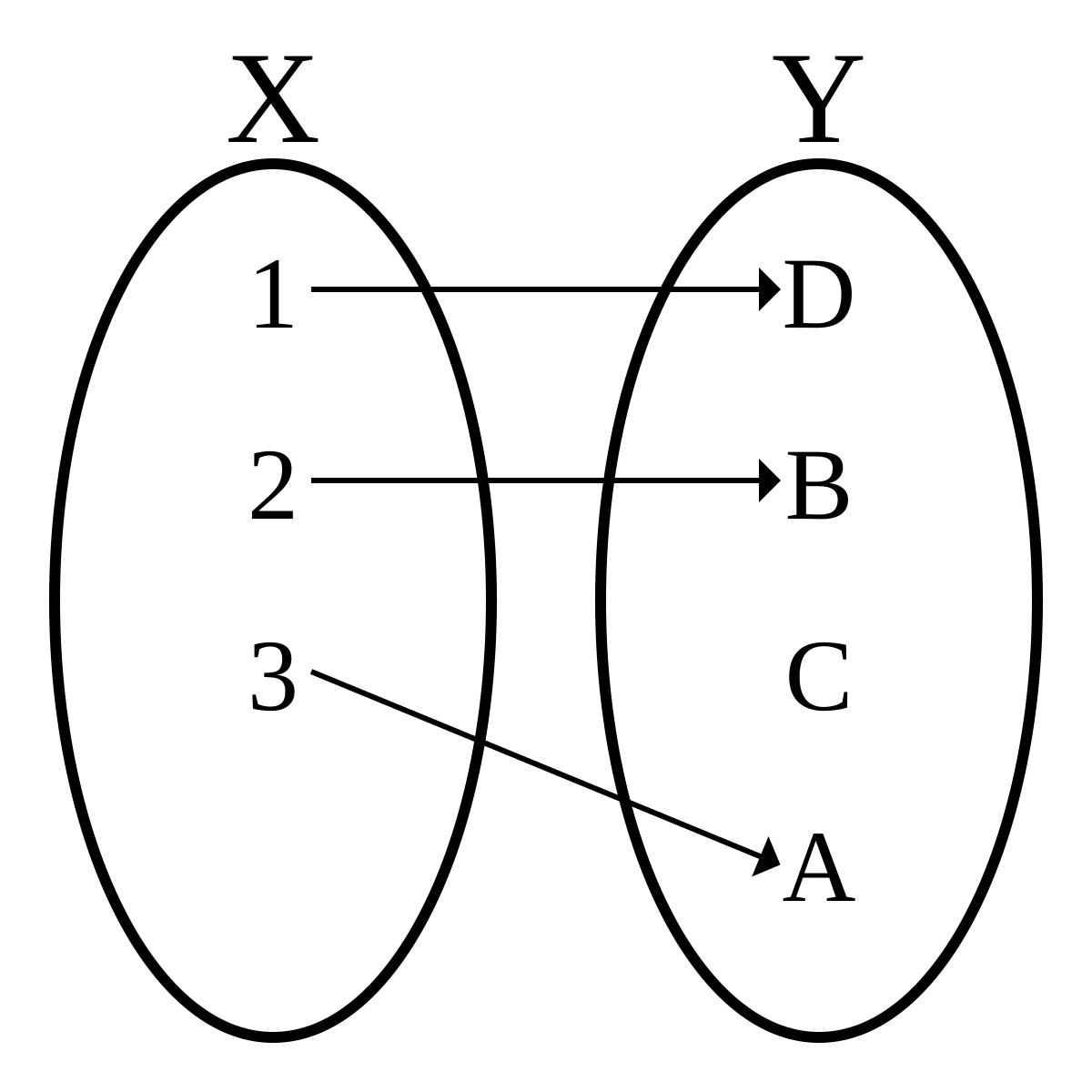



Injective Function Wikipedia
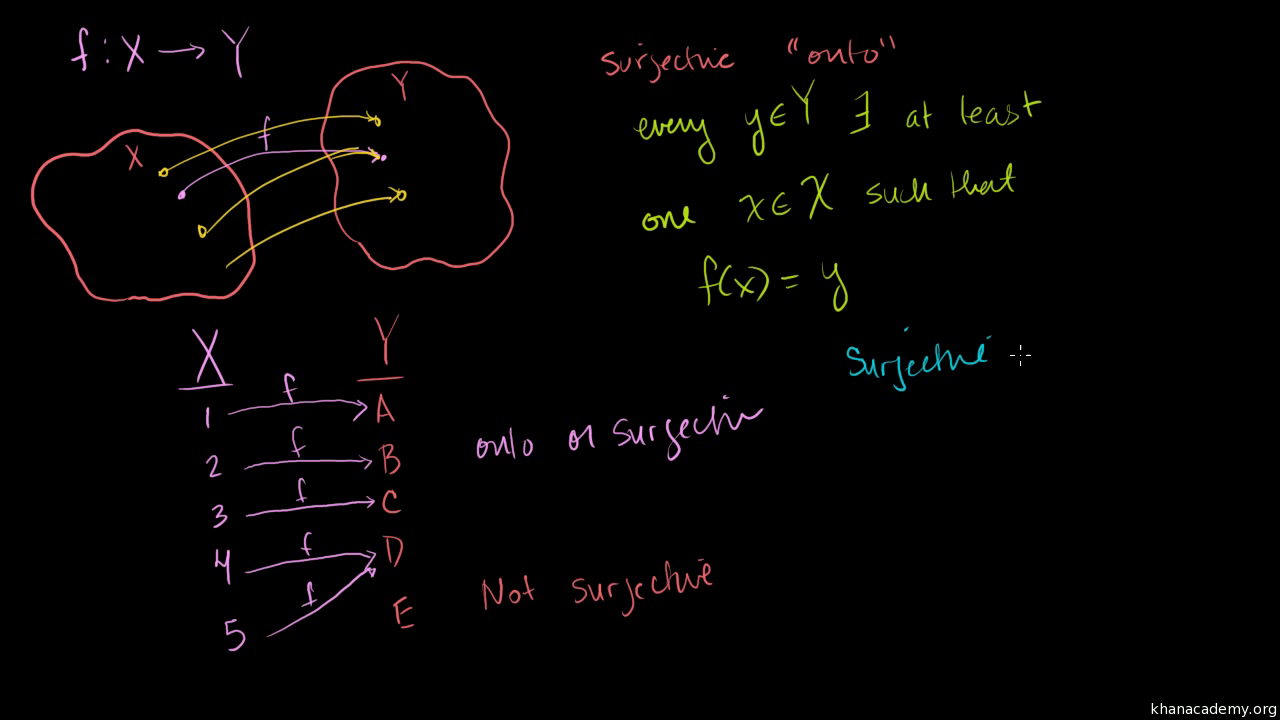



Surjective Onto And Injective One To One Functions Video Khan Academy




Show That Function F R X In R 1 X 1 Defined By F




Misc 4 Show F X X 1 X Is One One Onto Miscellaneous




The Function F R R F X X 2 Is A Injective But Not Surjectiv




Classify F R R Defined By F X X X 2 1 As Injection




Solved Let F X In X Squareroot X 2 1 Find The Doma Chegg Com




Ex 1 2 2 Check Injectivity And Surjectivity Of I F X X 2




Misc 4 Show F X X 1 X Is One One Onto Miscellaneous




Show That The Function F R R Given By F X X 3 X Is A Biject




F R 1 1 F X 10 X 10 X10 X 10 X Find F 1 If It Exists




Today S Topics Proof That A Given Function Is Injective Or Surjective Composite Functions Properties Of The Composite Functions Inverse Functions Proofs Ppt Download




Example 9 Prove That F X 2x Is One One And Onto Chapter 1




Answered 1 Let F R R Be Defined By F X 2x Bartleby




The Function F R 1 2 1 2 Defined As F X X 1 X 2 Is




Ex 1 2 10 F X X 2 X 3 Is F One One Onto Class 12




Vatrix Match Type Question Column I 12 F R R Defined By F X X 113 F




Show That The Function F N To N Defined By F X 2x 1 Is One One But Not Onto Brainly In




Ex 1 2 1 Class 12 Maths Show F X 1 X Is One One Onto Where R




If A Function F R To R Is Defined As F X X 2 1 Then Youtube




Pin On Proof Videos




Ex 1 2 2 Check Injectivity And Surjectivity Of I F X X 2




In Each Of The Following Cases State Whether The Function Is One




Example 10 Show F 1 F 2 1 And F X X 1 Is Onto



0 件のコメント:
コメントを投稿